We allocate objects to agents as exemplified primarily by school choice. Welfare judgments of the object-allocating agency are encoded as edge weights in the acceptability graph. The welfare of an allocation is the sum of its edge weights. We introduce the constrained welfare-maximizing solution, which is the allocation of highest welfare among the Pareto-efficient allocations. We identify conditions under which this solution is easily determined from a computational point of view. For the unrestricted case, we formulate an integer program and find this to be viable in practice as it quickly solves a real-world instance of kindergarten allocation and large-scale simulated instances. Incentives to report preferences truthfully are discussed briefly.
https://www.sciencedirect.com/science/article/pii/S0377221720302320?fbclid=IwAR3tHI9meDwq0F896ZtbTJM3VEk8T90AWeRy5fQYAC5BzS544AwICyhHuVo
A KRTK Közgazdaság-tudományi Intézet teljesítményéről A KRTK KTI a RePEc/IDEAS rangsorában, amely a világ közgazdaság-tudományi tanszékeit és intézeteit rangsorolja publikációs teljesítményük alapján, a legjobb ... Read More »
Tisztelt Kollégák! Tudományos kutatóként, intézeti vezetőként egész életünkben a kutatói szabadság és felelősség elve vezetett bennünket. Meggyőződésünk, hogy a tudomány csak akkor érhet el ... Read More »
Srí Lanka: a 2022-es gazdasági válság leckéje – A. Krueger Lessons from Sri Lanka Anne O. Krueger Jul 25, 2022 – Project Syndicate ... Read More »
A permanens válság korában élünk – J. Meadway We’re living in an age of permanent crisis – let’s stop planning for a ‘return ... Read More »
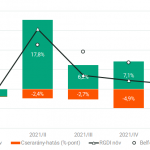
A 2021 végén, illetve 2022 elején tapaszalt 6, illetve 7%-os cserearányromlás brutális reáljövedelem-kivonást jelentett a magyar gazdaságból. A külső egyensúly alakulásával foglalkozó elemzések többnyire ... Read More »
