Al Roth és Lloyd Shapley professzorok közgazdasági Nobel-díjat kaptak a stabil párosítási témakörének elméleti vizsgálatáért és gyakorlati alkalmazásáért. Intézetünk játékelméleti kutatócsoportja számos tanulmányban foglalkozott a kérdéssel, három jelentős nemzetközi workshopot szervezett az elmúlt két évben, és két jelentős európai kutatási projektben is aktívan részt vesz, amelyek mind szorosan kötődnek a témakörhöz. Ezekről szeretnék beszámolni, többek között azért is, hogy a lehetséges kapcsolódási pontok mentén esetleg mások is csatlakozhassanak a kutatásainkhoz. Az ismertetést a három nemzetközi konferencia szerint bontva írom le, és a végére csatolok egy áttekintést a Computational Social Choice (magyarul társadalmi döntések számítástudománya, rövidítve COMSOC) tágabb témaköréről, amely teljes terjedelemben a Közgazdasági Szemlében [4] olvasható.
Idén júliusban a Corvinus Egyetemmel közösen rendeztük meg a MATCH-UP 2012 workshopot [21], amely a stabil párosítások témakörének eddigi talán legnagyobb interdiszciplináris konferenciája volt. Két neves közgazdász meghívott előadónk volt. Tayfun Sönmez, Al Roth egyik leggyakoribb társszerzője, aki az amerikai vesecsere-programok elméleti megalapozásában vele együtt részt vett, illetve az iskolaválasztási témakörének is az egyik legelismertebb szakértője. A konferencián az amerikai kadétok allokációs programjáról tartott egy érdekfeszítő előadást [17]. A másik meghívott előadó, Fuhito Kojima, Al Roth tanítványa volt a Harvardon. Workshopunkon arról tartott előadást [11], hogy az iskolaválasztási eljárás miként ösztönözheti az iskolákat a minőség növelésére a versenyhelyzetből kifolyólag.
2011 novemberében a Matching in Practice hálózat harmadik workshopja került megrendezésre intézetünkben [23]. A Matching in Practice európai kutatóhálózat [22] két éve alakult, célja, hogy egy fórumot biztosítson azon kutatóknak, akiket a párosításelmélet gyakorlati vonatkozásait kiemelten fontosnak tartják, és tevőlegesen is részt kívánnak venni ezen alkalmazások megtervezésében. A hálózat egyik konkrét célja, hogy összegyűjtse és elemezze az Európában működő központi párosító programokat az általános- és középiskolai, felsőoktatási felvételi eljárásokban és a kezdő munkavállalók (például rezidensek) allokációs mechanizmusaiban. Megjegyzem, hogy ennek előzményének tekinthető az a központi párosító alkalmazásokat összegyűjtő oldal, amit Glasgowban dolgozó kollégákkal szerkesztettünk 2008-ban, és amely frissített változata intézeti honlapunkon is megtalálható [18]. A hálózat vezetőinek másik kiemelt célja, hogy az elsősorban játékelmélettel foglalkozó közgazdászok mellett minél több társadalomtudományban és oktatásgazdaságtanban jártas szakember csatlakozzon a kutatómunkához. Ugyanis a központi párosító programok sikerességének megértéséhez nem csak magát az eljárást, hanem a gazdasági-társadalmi hátteret és hatásokat is fontos megismerni, elemezni. A következő workshop 2012 november közepén Barcelonában lesz, ahol már több szekcióban és egy kerekasztal-beszélgetésben is hallhatunk oktatásgazdaságtani szakértőket. Többek között Horn Dániel is előadást tart a kisgimnáziumok okozta társadalmi hatásokról.
A párosítási piacok tervezése szerves része egy új interdiszciplináris területnek, amit magyarul társadalmi döntések számítástudományának nevezhetünk. Intézetünkben erről tartottunk egy sikeres workshopot tavaly májusban [19], amelyről a már említett részletes beszámoló [4] készült. Aktuális hír, hogy egy európai COST projekt került elfogadásra a témában [20], amelyben csoportunkból ketten is részt veszünk (Kóczy Á. László és jómagam). A projekt négy munkacsoportja közül az egyik a párosítási problémákkal fog foglalkozni. A félévente tartott ülések és kutatói látogatások révén jó esély mutatkozik a szakmai együttműködések további fejlődésére. Az alakuló ülést november végén tartjuk Brüsszelben.
Amint a bevezetőmben ígértem, hadd csatoljam bejegyzésem végére a Közgazdasági Szemlében tavaly megjelent írásom [4] egy részletét, amelyben a COMSOC témakörét, és ezen belül is kiemelten a párosítási programok szerepét mutatom be.
A Computational Social Choice témakörének rövid bemutatása
Gazdasági vagy társadalmi szituációban gyakran előfordul, hogy a résztvevőknek valamilyen módon dönteniük kell arról, hogy milyen együttműködést hozzanak létre. Az együttműködés lehetséges formáit szabályozhatják törvényi előírások és íratlan társadalmi normák. Ugyanígy a döntési mechanizmusra is vonatkozhatnak keretfeltételek, amelyeket a részvevők elfogadnak. Ilyen helyzetekben a cél az, hogy a döntés eredménye valamilyen értelemben optimális és igazságos legyen a résztvevők valós preferenciáira nézve.
Vegyük például az iskolai felvételit. Itt a résztvevők a diákok (és a szüleik), az iskolák és a kormányzat (vagy önkormányzat) – mely utóbbi elviekben a társadalmi érdekeket képviseli. A döntés tárgya, hogy a diákok hová kerüljenek felvételre. A szereplőknek preferenciáik vannak a lehetséges megoldásokra nézve. Minden diák a számára legmegfelelőbb iskolába szeretne felvétel nyerni, az iskolák szeretnék feltölteni a kvótáikat a lehető legjobb diákokkal. A kormányzat célja már igen sokrétű lehet. Az általános iskolás és középiskolai felvételi esetén a legtöbb országban – így például a New York [1] és Boston városában [2] – a döntéshozók szerint a társadalmilag optimális és igazságos megoldásban a diákok prioritást kell, hogy kapjanak a lakóhelyükhöz közeli iskolákban, illetve ahová már legalább egy testvér jár a családjukból. A magyar középiskolai felvételiben ezzel szemben a kormányzat teljes mértékben az iskolákra bízza a felvételiző diákok rangsorolását.
A döntéshozatali mechanizmus működhet decentralizáltan vagy egy központi koordinátor (játékvezető) bevonásával. Decentralizált esetben egy szabályozott eljáráson keresztül alakul ki a megoldás, amelynek során a résztvevők stratégiai döntéseket hozhatnak. Egyetemi felvételi esetén például a legtöbb országban nincs központi adminisztráció, a diákok egyénileg dönthetnek, hogy hová jelentkeznek, és az intézmények is külön-külön hozzák meg döntésüket, hogy kit vesznek fel, a helyenként többfordulós felvételi eljárásban. Központi döntéshozatali mechanizmus esetén a résztvevők kinyilvánítják a preferenciáikat egy koordinátornak, amely ezek alapján – esetlegesen további objektív faktorokat figyelembe véve – automatikusan szolgáltatja az eredményt. A játékvezető nem csak személy, hanem egy automatikus mechanizmus is lehet, amely megjelenthet például egy internetes protokoll formájában.
Fontos kihangsúlyozni, hogy a szereplők által a döntéshozatali mechanizmus során követett stratégiák, illetve központi eljárásban a kinyilvánított preferenciák, nem feltétlenül vannak összhangban a valós preferenciákkal. E miatt a mechanizmus végén kapott eredmény sem biztos, hogy a valódi preferenciák szerint lesz optimális és igazságos. Ennek elkerülésére a döntési mechanizmusok tervezői igyekeznek olyan szabályrendszereket kialakítani, amely igazmondásra ösztönzi a résztvevőket. Ezt a kérdéskört leginkább a játékelmélet szakértői vizsgálják. A számítástudomány szerepe a mechanizmus-tervezési folyamatban a következő. A központi mechanizmusban jelenlévő automatizmus mögött általában egy optimalizáló algoritmus áll, melynek feladata, hogy a beérkező adatok függvényében hatékonyan adja meg a kívánatos végeredményt. Ez azonban nem mindig lehetséges, hiszen léteznek olyan optimalizálási problémák, amelyek bizonyítottan bonyolultak, ezekre hatékony algoritmus gyakorlatilag nem adható. Fontos tehát, hogy oly módon határozzuk meg az optimalitás feltételét, amelyre a kapott probléma algoritmikus értelemben kezelhető. Tágabb értelemben a társadalomtudomány, közgazdaságtan és játékelmélet feladata, hogy meghatározza milyen együttműködés tekinthető társadalmilag optimálisnak, igazságosnak egy adott szituációban.
Megjegyzem, hogy a központi koordináció a döntési mechanizmusokban nem jelent feltétlenül bürokratikus koordinációt, ahogyan azt Kornai [12] definiálta a koordinációs mechanizmusok kategorizálásakor. A témakör egyik legelismertebb közgazdásza, Roth [15] a következőképpen nyilatkozott erről a kérdésről az amerikai rezidensek allokálásra használt központi párosító programok kapcsán: „Vegyük észre, hogy az itt vizsgált központosított piacok nem jelentenek központosított tervezést, ahogyan a legtöbben ezt értelmezik, mivel ezek a piacok úgy lettek megalkotva, hogy érzékenyek legyenek a szereplők kinyilvánított preferenciáira, ahelyett, hogy egy tervező ezektől független céljainak elérését szolgálnák. Ami itt központosítva van, az nem az elérendő cél, hanem a piaci mechanizmus maga.”. A legtöbb esetben ez így is van, például az amerikai rezidensek programjában vagy a hazai középiskolai felvételi esetében. Vannak azonban arra is példák, hogy a kormányzati célok is részévé válnak az optimalizálási szempontoknak. A hazai felsőoktatási felvételiben a szakáganként meghatározott állami kvóták gazdasági érdekeket, a többletpontok rendszere – többek között – szociális érdekeket is szolgálhat. Egyébiránt a központi és bürokratikus koordináció kérdése nagyjából független attól, hogy a koordinációt állami szerv, független intézmény vagy magáncég szolgáltatja, mindegyikre akad példa a gyakorlatban.
Társadalmi döntési mechanizmusokra a legegyszerűbb és legrégebben alkalmazásban lévő eljárás a szavazás. Célja általában az alternatívák közti választás, a szavazatok aggregálásának módja azonban sokféle lehet. A koordinátor szerepe itt általában csak a szavazatok összeszámlálása, az eredmények összesítése. Ennek technikai megvalósítása az ókori cserépszavazástól napjainkra eljutott a teljesen automatizált webes szavazásig. Vannak azonban szituációk, amikor a koordinátor vagy egyes szereplők a szavazás lefolytatásának menetét is befolyásolhatják. Mind a szavazás menetének meghatározásakor, mind pedig a szavazáskor adódhatnak helyzetet, amikor a szereplők taktikázással számukra kedvezőbb eredményt érhetnek el. A legtöbb használatban lévő szavazási eljárásra igaz ugyanis, hogy a szavazóknak nem feltétlenül áll érdekükben a valós preferenciájuk szerinti szavazás.[1]
A piaci mechanizmusokat sokfajta koordinációs mechanizmus segítheti. A klasszikus piac – így a legtöbb áru és munkapiac – napjainkban is decentralizált, habár egyre kifinomultabb írott és íratlan szabályrendszer vonatkozik rájuk, nemzetközi szinten is. Emellett a koordinátorok szerepe is növekszik főként a modern technológia (elsősorban az Internet) adta lehetőségeknek köszönhetően. A piaci alkuszoknak már a középkorban [8] is jelentős szerepük volt abban, hogy a városi piacokon a vevők és eladók közötti kereskedés (ki kinek ad el és milyen áron) hatékony módon történjen. A piaci koordináció egy speciális esete az aukció, melyet a szakirodalom részletesen taglal. Az aukció vezetése napjainkban szintén egyre inkább webes portálok feladata, de az új technikai megoldástól függetlenül még mindig elkülönülnek a decentralizált eljárások – ahol a vásárlók az aktuális ár tudatában minden árura külön tesznek ajánlatot – illetve a központi mechanizmusok – ahol az ajánlatokat előre begyűjtik, és a megoldást a koordinátor határozza meg. Az előbbire egy modern példa az eBay, az utóbbira pedig a Google által koordinált aukció az amerikai televíziós hirdetésekre [13]. A résztvevők stratégiai döntései ezen alkufolyamatokban is megjelennek, de bizonyos alapesetekben a koordináció révén garantálható az optimális és igazságos eredmény elérése, amelyre a decentralizált piacokat mozgató „láthatatlan kéz” már nem mindig lenne képes.
Az én szakterületem a párosítások elmélete. A legelső ismert központi párosító programot az amerikai rezidensek elhelyezésére vezették be 1952-ben, amely révén minden évben körülbelül 30000 orvosjelöltet allokálnak kórházakhoz (lásd [14], [16]). Az itt is működő eljárás elméletét Gale és Shapley dolgozta ki [10] az egyetemi felvételik kontextusában. Az igazságosság feltételét a következő úgynevezett stabilitás fogalma adja: ha egy diák jelentkezését elutasítja egy egyetem, akkor ennek az oka csak az lehet, hogy az egyetem fel tudta tölteni helyeit az adott jelentkezőnél jobb diákokkal. Gale és Shapley belátta, hogy az általuk javasolt algoritmus minden esetben talál egy stabil párosítást, sőt ez a megoldás optimális a diákok részére (egyik diák sem kerülhet be jobb egyetemre semelyik stabil párosításban). Ez utóbbi állítás azt is eredményezi, hogy a diákoknak minden esetben megéri a valódi preferenciájukat megadni a jelentkezési lapon, mert taktikázással biztosan nem kerülhetnek be jobb helyre, vagyis az eljárás stratégiailag biztos. Végül az eljárás gyakorlati alkalmazhatóságának számítástudományi feltétele is teljesül: az algoritmus igen gyors, futásideje a jelentkezések számával arányos[2].
A fenti algoritmus működik a hazai középiskolai és egyetemi felvételi rendszerekben, és számos más alkalmazásban a világon. Ismertebb alkalmazások egy gyűjteménye megtalálható a kutatócsoportunk honlapján [18]. Jómagam, tevékenyen részt vettem az Egyesült Királyság vesecsere-programjának [8], a skóciai rezidensek allokációs programjának [6], valamint a magyar felsőoktatási felvételi rendszer pontszámítási eljárásának ([3], [5]) kidolgozásában és elemzésében. Az utóbbi két alkalmazásban használt párosító eljárások szintén a Gale-Shapley algoritmuson alapulnak, de mindkettőnek vannak speciális tulajdonságai, amelyek megnehezítik a problémát.
Hadd szemléltessem ezt egy konkrét esetben. Az amerikai rezidens allokációs programban a kilencvenes évek vége óta, Skóciában 2010 óta, házaspárok közös jelentkezési listát adhatnak le. Erre azért volt igény, mert az egy vagy két éves rezidensi időszakot a házaspárok nem szeretnék egymástól távol eltölteni, és így a többségük csak olyan pozíció-párokat jelöl be, amelyeket egymáshoz közel lévő kórházak írtak ki. Ez a speciális lehetőség azonban azt eredményezi, hogy többé nem garantált az igazságos megoldás létezése.[3] Sajnos az is belátható, hogy a stabil párosítás keresésének problémája NP-nehéz, így nem remélhető hatékony algoritmus ennek a feladatnak a kezelésére, az alkalmazásokban heurisztikák használata szükséges. Megjegyzem, hogy nagyon hasonló problémát okoz a hazai felsőoktatási felvételiben, hogy tanári szakokra párhuzamosan is lehet jelentkezni (például egy diák jelentkezhet egyszerre történelem és matematika tanári szak-párra).
Általánosan elmondható tehát, hogy párosítási problémák és piaci szituációk esetében is léteznek olyan eljárások, amelyek egy központi koordináció segítségével igazságos és optimális megoldásra vezetnek, ugyanis ez utóbbiak feltételei jól definiálhatóak, az eljárások stratégiailag biztosak és hatékonyan implementálhatók. Ennek köszönhető a párosító programok és bizonyos aukciós eljárások sikere és egyre szélesebb elterjedése. Elég azonban egyetlen speciális feltétel ahhoz, hogy a probléma elméleti értelemben bonyolulttá váljon, és a gyakorlatban heurisztikák alkalmazására kényszerüljenek a programok tervezői.
Irodalom
[1] A. Abdulkadiroglu, P.A. Pathak and A.E. Roth, T. Sönmez (2005): The New York Public School Match. American Economic Review, 95, pp. 364-367
[3] P. Biró (2008): Student Admissions in Hungary as Gale and Shapley Envisaged. Technical Report no. TR-2008-291 of the Computing Science Department of Glasgow University
[5] P. Biró, T. Fleiner, R.W. Irving and D.F. Manlove: The College Admissions problem with lower and common quotas. Theoretical Computer Science, 411, pp. 3136-3153
[6] P. Biró, R.W. Irving and I. Schlotter (2011): Stable matching with couples – an empirical study. ACM Journal of Experimental Algorithmics, 16, Article number 1.2
[7] P. Biró, F. Klijn, Matching with Couples: a Multidisciplinary Survey. To appear in International Game Theory Review (2012).
[8] P. Biró, D.F. Manlove and R. Rizzi (2009): Maximum weight cycle packing in directed graphs, with application to kidney exchange programs. Discrete Mathematics, Algorithms and Applications, 1, 499-517
[9] L. Börner and D. Quint (2010): Medieval Matching Markets. Discussion Papers, Freie Universität Berlin, School of Business and Economics, 2010/31.
[12] J. Kornai (1983): Bürokratikus és piaci koordináció. Közgazdasági Szemle, 30, 1025-1038
[14]A.E. Roth (1984): The Evolution of the Labor Market for Medical Interns and Residents: A Case Study in Game Theory. Journal of Political Economy, 92, 1984, 991-1016
[16] A.E. Roth (2008): Deferred Acceptance Algorithms: History, Theory, Practice, and Open Questions. International Journal of Game Theory , 36, 537-569
[18] Website of applications: http://econ.core.hu/english/res/game_app.html
[19] Website of COMSOC workshop: http://econ.core.hu/english/res/game_comsoc.html
[20]Website of the COMSOC COST project, Memorandum of Understanding: http://w3.cost.eu/fileadmin/domain_files/ICT/Action_IC1205/mou/IC1205-e.pdf
[21]Website of MATCH-UP 2012 workshop: http://econ.core.hu/english/res/MATCH-UP_2012.html
[22]Website of Matching in Practice network: http://www.matching-in-practice.eu/
Website of the Third Matching in Practice workshop, held at our institute: http://econ.core.hu/english/res/game_Matching_in_Practice.html
[1]Vegyük egyszerű példaként a hazai parlamenti választásokat. A listás szavazat leadásakor az a szavazó, aki olyan pártot favorizál, amely a bekerülési küszöbhöz (5%) közeli támogatással bír, esetleg elgondolkozik azon, hogy ne kockáztassa a szavazata elveszítését, és inkább egy kevésbé kedvelt, de biztos befutó pártra szavaz.
[2]Hazánkban például a felsőoktatási felvételiben használt pontszámító algoritmus körülbelül 10 másodperc alatt végez a számítással, ami azt jelenti, hogy ugyanez a program mondjuk az Egyesült Királyság felvételijére futtatva – ahol a jelentkezők és a jelentkezések száma is nagyjából hatszoros – körülbelül egy perc alatt végezne. Megjegyzem, hogy ha a futásidő lineárisnál lényegesen rosszabb, például négyzetes vagy köbös volna, akkor már nem biztos, hogy alkalmazható lenne ilyen nagy méretű feladatok megoldására.
[3] Lássunk erre egy példát. Éva és Ádám egy házaspár, akik csak az (X,Y) kórház-párt jelölik meg a közös listájukon, vagyis ha Éva megkapja az állást X-ben és Ádám Y-ban, akkor ezt elfogadják, egyébként inkább várnak még egy évet (vagy külföldre mennek). A harmadik orvos, Béla preferencia listája szintén az X és Y kórházakat tartalmazza, ebben a sorrendben. A kórházak egyetértenek abban, hogy Éva a legjobb orvos, Béla a második legjobb és Ádám a harmadik. Van-e igazságos megoldás? Ha a házaspárt allokáljuk a kórházakba, akkor az Y kórház joggal élhet panasszal, hiszen inkább Bélát venné fel Ádám helyett, ugyanis ő egy jobb orvos. Ha viszont nem allokáljuk a házaspárt, és Bélát veszi fel Y, akkor Béla és – a pillanatnyilag senkit sem foglalkoztató – X kórház köthetne egy új szerződést, amivel mindkét fél jobban járna. Végül, ha Bélát X-be allokáljuk, akkor mindkét kórház jobban járna a házaspár felvételével, ugyanis Évát jobb orvosnak gondolják X-ben mint Bélát, Y-ban pedig senki sincs felvéve.
Nem található esemény a közeljövőben.
A KRTK Közgazdaság-tudományi Intézet teljesítményéről A KRTK KTI a RePEc/IDEAS rangsorában, amely a világ közgazdaság-tudományi tanszékeit és intézeteit rangsorolja publikációs teljesítményük alapján, a legjobb ... Read More »

Tisztelt Kollégák! Tudományos kutatóként, intézeti vezetőként egész életünkben a kutatói szabadság és felelősség elve vezetett bennünket. Meggyőződésünk, hogy a tudomány csak akkor érhet el ... Read More »

Srí Lanka: a 2022-es gazdasági válság leckéje – A. Krueger Lessons from Sri Lanka Anne O. Krueger Jul 25, 2022 – Project Syndicate ... Read More »

A permanens válság korában élünk – J. Meadway We’re living in an age of permanent crisis – let’s stop planning for a ‘return ... Read More »
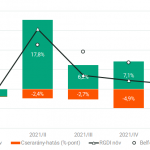
A 2021 végén, illetve 2022 elején tapaszalt 6, illetve 7%-os cserearányromlás brutális reáljövedelem-kivonást jelentett a magyar gazdaságból. A külső egyensúly alakulásával foglalkozó elemzések többnyire ... Read More »
