 link.springer.com
link.springer.com
Cseh Ágnes tudományos munkatárs és Telikepalli Kavitha közös cikke Popular edges and dominant matchings címmel megjelent a Mathematical programming folyóiratban.
Abstract
Given a bipartite graph G=(A∪B,E) with strict preference lists and given an edge e∗∈E , we ask if there exists a popular matching in G that contains e∗ . We call this the popular edge problem. A matching M is popular if there is no matching M′ such that the vertices that prefer M′ to M outnumber those that prefer M to M′ . It is known that every stable matching is popular; however G may have no stable matching with the edge e∗ . In this paper we identify another natural subclass of popular matchings called “dominant matchings” and show that if there is a popular matching that contains the edge e∗ , then there is either a stable matching that contains e∗ or a dominant matching that contains e∗ . This allows us to design a linear time algorithm for identifying the set of popular edges. When preference lists are complete, we show an O(n3) algorithm to find a popular matching containing a given set of edges or report that none exists, where n=|A|+|B| .
Nem található esemény a közeljövőben.
A KRTK Közgazdaság-tudományi Intézet teljesítményéről A KRTK KTI a RePEc/IDEAS rangsorában, amely a világ közgazdaság-tudományi tanszékeit és intézeteit rangsorolja publikációs teljesítményük alapján, a legjobb ... Read More »

Tisztelt Kollégák! Tudományos kutatóként, intézeti vezetőként egész életünkben a kutatói szabadság és felelősség elve vezetett bennünket. Meggyőződésünk, hogy a tudomány csak akkor érhet el ... Read More »

Srí Lanka: a 2022-es gazdasági válság leckéje – A. Krueger Lessons from Sri Lanka Anne O. Krueger Jul 25, 2022 – Project Syndicate ... Read More »

A permanens válság korában élünk – J. Meadway We’re living in an age of permanent crisis – let’s stop planning for a ‘return ... Read More »
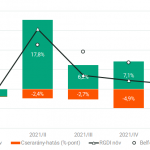
A 2021 végén, illetve 2022 elején tapaszalt 6, illetve 7%-os cserearányromlás brutális reáljövedelem-kivonást jelentett a magyar gazdaságból. A külső egyensúly alakulásával foglalkozó elemzések többnyire ... Read More »
