
Biró Péter tudományos főmunkatárs, Walter Kern, Danial Paulusma és Wojuteczky Péter közös cikke The stable fixtures problem with payments címmel megjelent a Games and Economic Behavior folyóiratban.
We consider multiple partners matching games (G,b,w), where G is a graph with an integer vertex capacity function b and an edge weighting w. If G is bipartite, these games are called multiple partners assignment games. We give a polynomial-time algorithm that either finds that a given multiple partners matching game has no stable solution, or obtains a stable solution. We characterize the set of stable solutions of a multiple partners matching game in two different ways and show how this leads to simple proofs for a number of results of Sotomayor, 1992, Sotomayor, 1999, Sotomayor, 2007 for multiple partners assignment games and to generalizations of some of these results to multiple partners matching games. We also perform a study on the core of multiple partners matching games. We prove that the problem of deciding if an allocation belongs to the core jumps from being polynomial-time solvable for b≤2 to NP-complete for b≡3.
Nem található esemény a közeljövőben.
A KRTK Közgazdaság-tudományi Intézet teljesítményéről A KRTK KTI a RePEc/IDEAS rangsorában, amely a világ közgazdaság-tudományi tanszékeit és intézeteit rangsorolja publikációs teljesítményük alapján, a legjobb ... Read More »

Tisztelt Kollégák! Tudományos kutatóként, intézeti vezetőként egész életünkben a kutatói szabadság és felelősség elve vezetett bennünket. Meggyőződésünk, hogy a tudomány csak akkor érhet el ... Read More »

Srí Lanka: a 2022-es gazdasági válság leckéje – A. Krueger Lessons from Sri Lanka Anne O. Krueger Jul 25, 2022 – Project Syndicate ... Read More »

A permanens válság korában élünk – J. Meadway We’re living in an age of permanent crisis – let’s stop planning for a ‘return ... Read More »
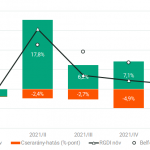
A 2021 végén, illetve 2022 elején tapaszalt 6, illetve 7%-os cserearányromlás brutális reáljövedelem-kivonást jelentett a magyar gazdaságból. A külső egyensúly alakulásával foglalkozó elemzések többnyire ... Read More »
